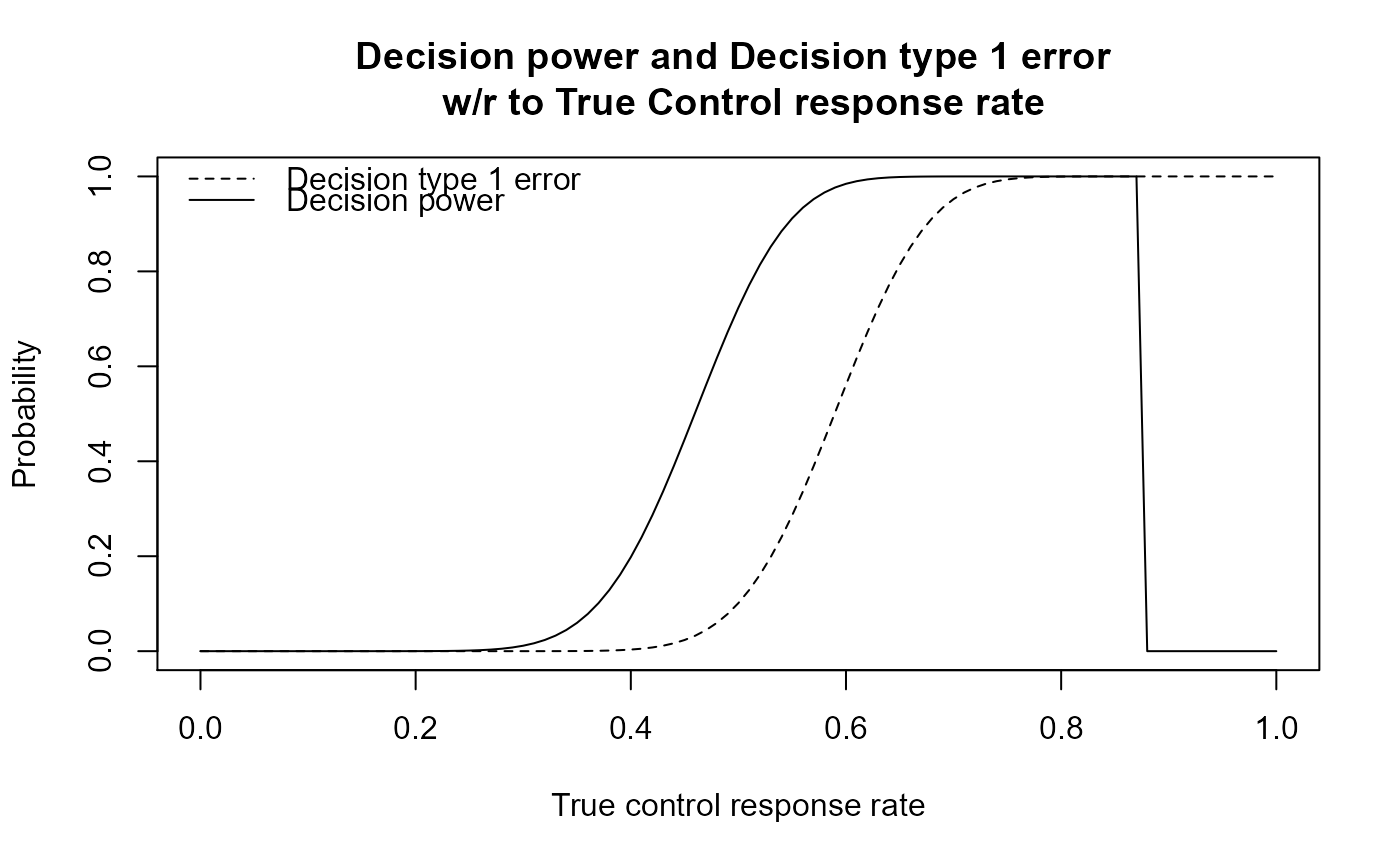
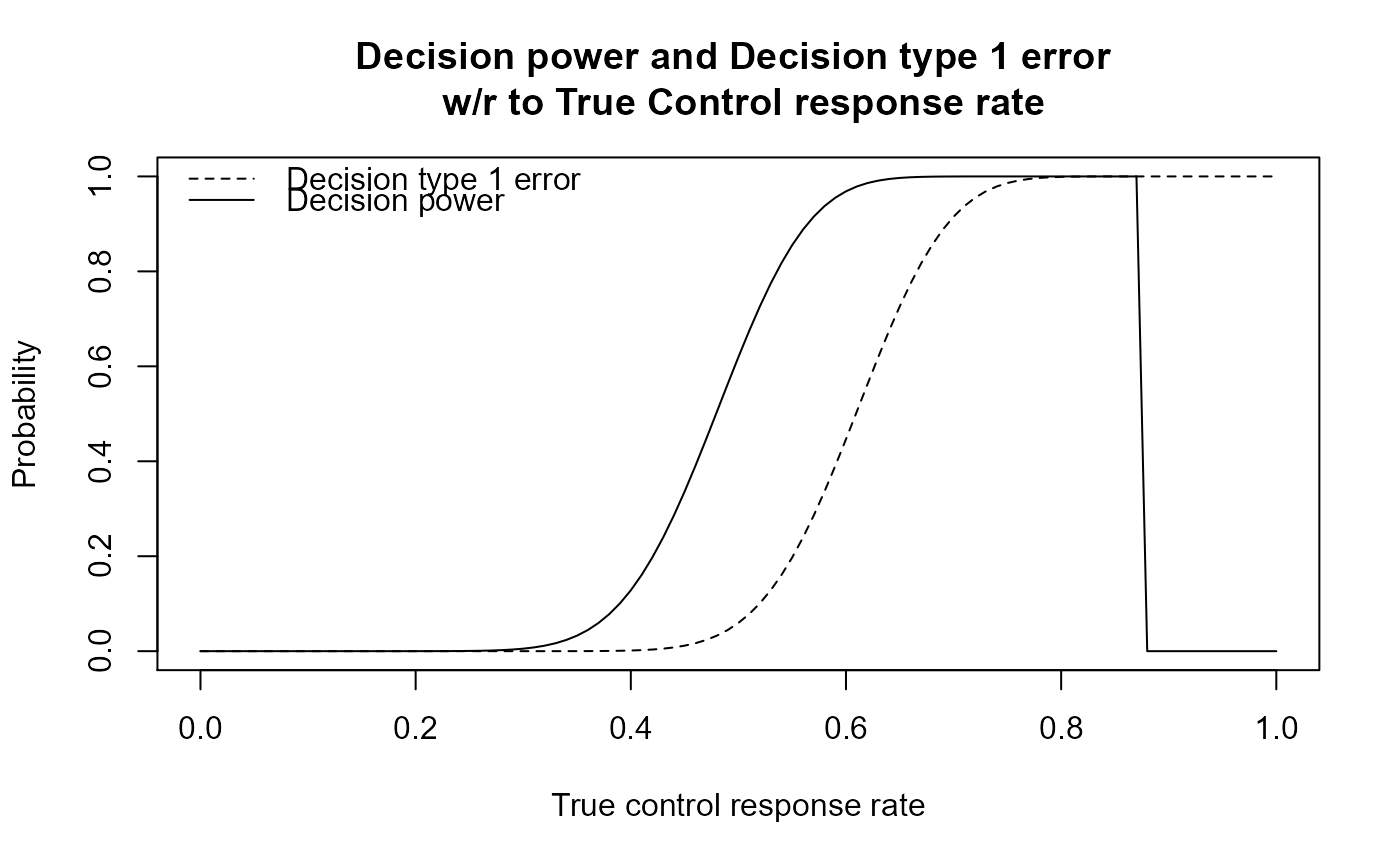
Single Arm Operating Characteristics
oc.RdFunction for calculating the operating characteristics of the single arm Bayesian designs in setting 1 and 2 for early gating.
oc( N_e, delta, delta_power, confidence, e_a = 0.5, e_b = 0.5, h_a = 0.5, h_b = 0.5, RR_h = NULL, N_h = NULL, hist_RR_c = NULL, trues = seq(0, 1, 0.01), adapt = 1, plot = T, legend = T, legend.pos = "topleft" )
Arguments
| N_e | Sample Size in the experimental group. Can be either a single value or a vector. |
|---|---|
| delta | Required superiority to make a "GO" decision. Corresponds to \(\delta\). |
| delta_power | Superiority, at which decision power will be evaluated. Corresponds to \(\bar{\delta}\). |
| confidence | Required confidence to make "GO" decision. Corresponds to \(\gamma\). |
| e_a | Alpha parameter of Beta Prior Distribution for the experimental response rate. Corresponds to \(\alpha_e\). Default is \(\frac{1}{2}\). |
| e_b | Beta parameter of Beta Prior Distribution for the experimental response rate. Corresponds to \(\beta_e\). Default is \(\frac{1}{2}\). |
| h_a | Alpha parameter of Beta Prior Distribution for the historical control response rate. Corresponds to \(\alpha_h\). Only needs to be specified, if RR_h and N_h are also specified. Default is \(\frac{1}{2}\). |
| h_b | Beta parameter of Beta Prior Distribution for the historical control response rate. Corresponds to \(\beta_h\). Only needs to be specified, if RR_h and N_h are also specified. Default is \(\frac{1}{2}\). |
| RR_h | Historical control response rate. Corresponds to \(p_h\). If specified together with N_h, function will use setting 2 from pdf. |
| N_h | Historical control sample size. Corresponds to \(n_h\). If specified together with RR_h, function will use setting 2 from pdf. |
| hist_RR_c | Point estimate of historical control repsonse rate. Corresponds to \(\hat{p_h}\). If specified, while RR_h and N_h are not specified, function will use setting 1 from pdf. |
| trues | Sequence of true control response rates and experimental response rates, at which the Probability to Go will be computed. Default is seq(0,1,0.01) to ensure continuous plots and accurate results. |
| adapt | Level of adapting of experimental control rate to account for patient selection bias from phase II to phase III. Corresponds to \(\xi\). Default is 1, so no adapting. |
| plot | Plots yes or no. Default is TRUE. |
| legend | Logical; whether or not to include legend in plot. Default is TRUE. |
| legend.pos | Position of legend. Default is "topleft". |
Value
A matrix containing the decision power and decision alpha with respect to the true control response rate.
Examples
# Setting 1 oc( N_e = 50, delta = 0.08, delta_power = 0.13, confidence = 0.6, hist_RR_c = 0.5 )#> Dec. Alpha Dec. Power True Control RR #> [1,] 0.0000 0.0000 0.00 #> [2,] 0.0000 0.0000 0.01 #> [3,] 0.0000 0.0000 0.02 #> [4,] 0.0000 0.0000 0.03 #> [5,] 0.0000 0.0000 0.04 #> [6,] 0.0000 0.0000 0.05 #> [7,] 0.0000 0.0000 0.06 #> [8,] 0.0000 0.0000 0.07 #> [9,] 0.0000 0.0000 0.08 #> [10,] 0.0000 0.0000 0.09 #> [11,] 0.0000 0.0000 0.10 #> [12,] 0.0000 0.0000 0.11 #> [13,] 0.0000 0.0000 0.12 #> [14,] 0.0000 0.0000 0.13 #> [15,] 0.0000 0.0000 0.14 #> [16,] 0.0000 0.0000 0.15 #> [17,] 0.0000 0.0000 0.16 #> [18,] 0.0000 0.0000 0.17 #> [19,] 0.0000 0.0000 0.18 #> [20,] 0.0000 0.0000 0.19 #> [21,] 0.0000 0.0001 0.20 #> [22,] 0.0000 0.0002 0.21 #> [23,] 0.0000 0.0003 0.22 #> [24,] 0.0000 0.0005 0.23 #> [25,] 0.0000 0.0008 0.24 #> [26,] 0.0000 0.0013 0.25 #> [27,] 0.0000 0.0021 0.26 #> [28,] 0.0000 0.0034 0.27 #> [29,] 0.0000 0.0052 0.28 #> [30,] 0.0000 0.0078 0.29 #> [31,] 0.0000 0.0115 0.30 #> [32,] 0.0000 0.0166 0.31 #> [33,] 0.0000 0.0235 0.32 #> [34,] 0.0001 0.0327 0.33 #> [35,] 0.0002 0.0446 0.34 #> [36,] 0.0003 0.0596 0.35 #> [37,] 0.0005 0.0784 0.36 #> [38,] 0.0008 0.1013 0.37 #> [39,] 0.0013 0.1287 0.38 #> [40,] 0.0021 0.1609 0.39 #> [41,] 0.0034 0.1980 0.40 #> [42,] 0.0052 0.2398 0.41 #> [43,] 0.0078 0.2862 0.42 #> [44,] 0.0115 0.3365 0.43 #> [45,] 0.0166 0.3901 0.44 #> [46,] 0.0235 0.4461 0.45 #> [47,] 0.0327 0.5035 0.46 #> [48,] 0.0446 0.5610 0.47 #> [49,] 0.0596 0.6176 0.48 #> [50,] 0.0784 0.6722 0.49 #> [51,] 0.1013 0.7236 0.50 #> [52,] 0.1287 0.7711 0.51 #> [53,] 0.1609 0.8139 0.52 #> [54,] 0.1980 0.8518 0.53 #> [55,] 0.2398 0.8844 0.54 #> [56,] 0.2862 0.9118 0.55 #> [57,] 0.3365 0.9343 0.56 #> [58,] 0.3901 0.9522 0.57 #> [59,] 0.4461 0.9662 0.58 #> [60,] 0.5035 0.9768 0.59 #> [61,] 0.5610 0.9845 0.60 #> [62,] 0.6176 0.9900 0.61 #> [63,] 0.6722 0.9937 0.62 #> [64,] 0.7236 0.9962 0.63 #> [65,] 0.7711 0.9978 0.64 #> [66,] 0.8139 0.9988 0.65 #> [67,] 0.8518 0.9994 0.66 #> [68,] 0.8844 0.9997 0.67 #> [69,] 0.9118 0.9998 0.68 #> [70,] 0.9343 0.9999 0.69 #> [71,] 0.9522 1.0000 0.70 #> [72,] 0.9662 1.0000 0.71 #> [73,] 0.9768 1.0000 0.72 #> [74,] 0.9845 1.0000 0.73 #> [75,] 0.9900 1.0000 0.74 #> [76,] 0.9937 1.0000 0.75 #> [77,] 0.9962 1.0000 0.76 #> [78,] 0.9978 1.0000 0.77 #> [79,] 0.9988 1.0000 0.78 #> [80,] 0.9994 1.0000 0.79 #> [81,] 0.9997 1.0000 0.80 #> [82,] 0.9998 1.0000 0.81 #> [83,] 0.9999 1.0000 0.82 #> [84,] 1.0000 1.0000 0.83 #> [85,] 1.0000 1.0000 0.84 #> [86,] 1.0000 1.0000 0.85 #> [87,] 1.0000 1.0000 0.86 #> [88,] 1.0000 1.0000 0.87 #> [89,] 1.0000 0.0000 0.88 #> [90,] 1.0000 0.0000 0.89 #> [91,] 1.0000 0.0000 0.90 #> [92,] 1.0000 0.0000 0.91 #> [93,] 1.0000 0.0000 0.92 #> [94,] 1.0000 0.0000 0.93 #> [95,] 1.0000 0.0000 0.94 #> [96,] 1.0000 0.0000 0.95 #> [97,] 1.0000 0.0000 0.96 #> [98,] 1.0000 0.0000 0.97 #> [99,] 1.0000 0.0000 0.98 #> [100,] 1.0000 0.0000 0.99 #> [101,] 1.0000 0.0000 1.00# Setting 2 oc( N_e = 50, delta = 0.08, delta_power = 0.13, confidence = 0.6, RR_h = 0.5, N_h = 50 )#> Dec. Alpha Dec. Power True Control RR #> [1,] 0.0000 0.0000 0.00 #> [2,] 0.0000 0.0000 0.01 #> [3,] 0.0000 0.0000 0.02 #> [4,] 0.0000 0.0000 0.03 #> [5,] 0.0000 0.0000 0.04 #> [6,] 0.0000 0.0000 0.05 #> [7,] 0.0000 0.0000 0.06 #> [8,] 0.0000 0.0000 0.07 #> [9,] 0.0000 0.0000 0.08 #> [10,] 0.0000 0.0000 0.09 #> [11,] 0.0000 0.0000 0.10 #> [12,] 0.0000 0.0000 0.11 #> [13,] 0.0000 0.0000 0.12 #> [14,] 0.0000 0.0000 0.13 #> [15,] 0.0000 0.0000 0.14 #> [16,] 0.0000 0.0000 0.15 #> [17,] 0.0000 0.0000 0.16 #> [18,] 0.0000 0.0000 0.17 #> [19,] 0.0000 0.0000 0.18 #> [20,] 0.0000 0.0000 0.19 #> [21,] 0.0000 0.0000 0.20 #> [22,] 0.0000 0.0000 0.21 #> [23,] 0.0000 0.0001 0.22 #> [24,] 0.0000 0.0002 0.23 #> [25,] 0.0000 0.0003 0.24 #> [26,] 0.0000 0.0005 0.25 #> [27,] 0.0000 0.0008 0.26 #> [28,] 0.0000 0.0014 0.27 #> [29,] 0.0000 0.0022 0.28 #> [30,] 0.0000 0.0034 0.29 #> [31,] 0.0000 0.0053 0.30 #> [32,] 0.0000 0.0079 0.31 #> [33,] 0.0000 0.0116 0.32 #> [34,] 0.0000 0.0167 0.33 #> [35,] 0.0000 0.0236 0.34 #> [36,] 0.0001 0.0327 0.35 #> [37,] 0.0002 0.0445 0.36 #> [38,] 0.0003 0.0595 0.37 #> [39,] 0.0005 0.0781 0.38 #> [40,] 0.0008 0.1009 0.39 #> [41,] 0.0014 0.1282 0.40 #> [42,] 0.0022 0.1604 0.41 #> [43,] 0.0034 0.1974 0.42 #> [44,] 0.0053 0.2392 0.43 #> [45,] 0.0079 0.2857 0.44 #> [46,] 0.0116 0.3362 0.45 #> [47,] 0.0167 0.3901 0.46 #> [48,] 0.0236 0.4465 0.47 #> [49,] 0.0327 0.5043 0.48 #> [50,] 0.0445 0.5624 0.49 #> [51,] 0.0595 0.6195 0.50 #> [52,] 0.0781 0.6745 0.51 #> [53,] 0.1009 0.7264 0.52 #> [54,] 0.1282 0.7743 0.53 #> [55,] 0.1604 0.8174 0.54 #> [56,] 0.1974 0.8553 0.55 #> [57,] 0.2392 0.8879 0.56 #> [58,] 0.2857 0.9152 0.57 #> [59,] 0.3362 0.9374 0.58 #> [60,] 0.3901 0.9551 0.59 #> [61,] 0.4465 0.9686 0.60 #> [62,] 0.5043 0.9788 0.61 #> [63,] 0.5624 0.9861 0.62 #> [64,] 0.6195 0.9912 0.63 #> [65,] 0.6745 0.9946 0.64 #> [66,] 0.7264 0.9969 0.65 #> [67,] 0.7743 0.9982 0.66 #> [68,] 0.8174 0.9991 0.67 #> [69,] 0.8553 0.9995 0.68 #> [70,] 0.8879 0.9998 0.69 #> [71,] 0.9152 0.9999 0.70 #> [72,] 0.9374 1.0000 0.71 #> [73,] 0.9551 1.0000 0.72 #> [74,] 0.9686 1.0000 0.73 #> [75,] 0.9788 1.0000 0.74 #> [76,] 0.9861 1.0000 0.75 #> [77,] 0.9912 1.0000 0.76 #> [78,] 0.9946 1.0000 0.77 #> [79,] 0.9969 1.0000 0.78 #> [80,] 0.9982 1.0000 0.79 #> [81,] 0.9991 1.0000 0.80 #> [82,] 0.9995 1.0000 0.81 #> [83,] 0.9998 1.0000 0.82 #> [84,] 0.9999 1.0000 0.83 #> [85,] 1.0000 1.0000 0.84 #> [86,] 1.0000 1.0000 0.85 #> [87,] 1.0000 1.0000 0.86 #> [88,] 1.0000 1.0000 0.87 #> [89,] 1.0000 0.0000 0.88 #> [90,] 1.0000 0.0000 0.89 #> [91,] 1.0000 0.0000 0.90 #> [92,] 1.0000 0.0000 0.91 #> [93,] 1.0000 0.0000 0.92 #> [94,] 1.0000 0.0000 0.93 #> [95,] 1.0000 0.0000 0.94 #> [96,] 1.0000 0.0000 0.95 #> [97,] 1.0000 0.0000 0.96 #> [98,] 1.0000 0.0000 0.97 #> [99,] 1.0000 0.0000 0.98 #> [100,] 1.0000 0.0000 0.99 #> [101,] 1.0000 0.0000 1.00